구랩

from pmdarima.arima import auto_arima

auto_arima_result = auto_arima(airDF, start_p = 1, start_q = 1, max_p = 3, max_q = 3,
          seasonal = True, d = 1, D=1, m=12, start_P = 1, start_Q = 1, max_P = 3, max_Q = 3, trace=True,
          error_action = 'ignore', suppress_warnings = True, stepwise=False)

1. 시계열

통계학에서 시계열 데이터 분석은 a변수로 b변수를 예측하는 것이 아닌 b변수의 과거데이터들을 이용하여 미래 시점을 예측하게 된다. t-1,...,t-n 시점의 데이터들을 이용해서 t시점의 데이터들을 예측하게 된다.

2. 분해법

데이터

airDF = pd.read_csv('international-airline-passengers.txt',
                   parse_dates=['time'], index_col='time')
airDF.head(3)

월별 주기로 이루어져있는 데이터

from statsmodels.tsa.seasonal import seasonal_decompose

result = seasonal_decompose(airDF, freq=12, model = 'addictibve')
# result = seasonal_decompose(airDF-1, freq=12, model = 'multiplicativbe')

result.plot()
plt.show()


# result.observed 관찰값
# result.trend 추세성분
# result.seasonal 계절성분
# result.resid 잔차

분해법은 시계열의 성분이 어떠한 패턴을 가지고 이루어져있을 것이라는 가정하에

Zt = Tt (추세성분 : 장기적인 변동) +

       St (계절성분 : 주별, 월별, 분기별 처럼 주기가짧은 규칙적으로 반복되는 변동)+

       Ct (순환성분 : 계절성분과 유사하다나 구기가 김, 많은 경우 분해법을 적용할 때 포함하지 않ㅇ므)  +

       It (불규칙성분 )

위처럼 분해하여 설명하는 모형이다. 각 성분을 잇는것이 +이냐 * 이냐에 따라

가법모형과 승법모형으로 나뉘게 된다 .

3. ARIMA

acf, pacf

from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

def plot_ts_corr(ts):
    fig, axes= plt.subplots(1,2, figsize = (10, 4))
    plot_acf(ts, ax = axes[0], lags = 30)
    plot_pacf(ts, ax = axes[1], lags = 30)
    plt.show()
    
plot_ts_corr(airDF)

자기상관계수 : 자신의 t시점차이의 데이터와의 상관계수 x축은 시점 y축은 상관계수값

부분자기상관계수 : 자신의 t시점차이의 데이터와의 상관계수 단, t시점과 시차가 n인 상관계수값은 시차가 1인 데이터 시차가 2인데이터 ... 시차가 n-1 인데이터들의 영향을 제거하여 계산

x축은 시점 y축은 상관계수값

위 그래프를 보고 arima모델의 pdq를 예측함

정상성

arima 모델을 적용하려면 정상시계열이라는 조건이 필요하다.

정상시계열이란 

E(Xt)가 t의 값과 상관없이 일정

Var(Xt)가 존재하고 t의 값에 상관없이 일정

Cov(Xt, Xt+h)가 t와는 무관하고 h(시차)의 값에만 의존 

위 조건을 만족하는 시계열 데이터이다.

예시 데이터는 진폭이 일정하지않고 (분산이 일정하지 않고) 평균값이 시차에 의존하는것으로 보이기 때문에 비정상시계열일 것이다. 추가적으로 정상성을 만족하는지 확인하는 검정과정을 ㅅ행한다

from statsmodels.tsa.stattools import adfuller

def adfuller_test(ts):
    test = adfuller(ts, maxlag=12)[:2]
    print('*** adfuller-test *** \n alternative hypothesis: stationary \n statistic = %6.3f p-value = %6.4f\n' % test)
    
adfuller_test(airDF)

*** adfuller-test *** 
 alternative hypothesis: stationary 
 statistic =  1.565 p-value = 0.9977

pvalue가 아주 높으므로 정상성을 띈다는 대립가설을 기각한다. 즉 위의 데이터는 비정상 시계열이다.

정상성을 만족하게 하는 방법은 여러가지가 있지만 보통 차분을 사용한다.

fig, axes= plt.subplots(2,1, figsize = (10, 6))

axes[0].plot(airDF, color = 'red')
axes[0].legend(['before diff'])
axes[1].plot(airDF.diff(1))
axes[1].legend(['after diff'])
plt.show()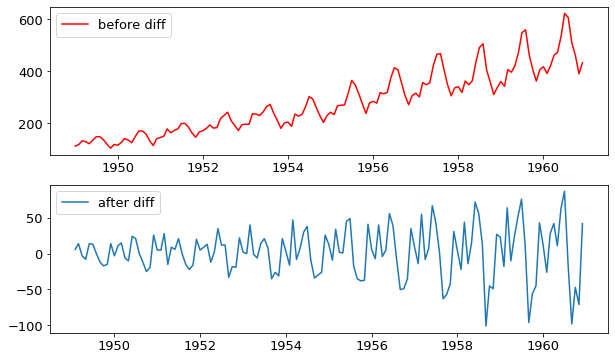

차분 이후에도 분산이 점점 시간이 지남에 따라 커지는 것으로 보아 아직 정상시계열이 아닌것으로 보이지만 위와 같은 방법으로 차분을 실시할 수 있다.

시계열 데이터가 정상시계열이라는 가정하에 (차분을 거치며 테스트로 확인 차분횟수  = d)

위의 표의 기준으로 차수를 결정이후

from statsmodels.tsa.arima.model import ARIMA

arima_res = ARIMA(airDF, order=(1, 1, 0)).fit()
arima_res.summary()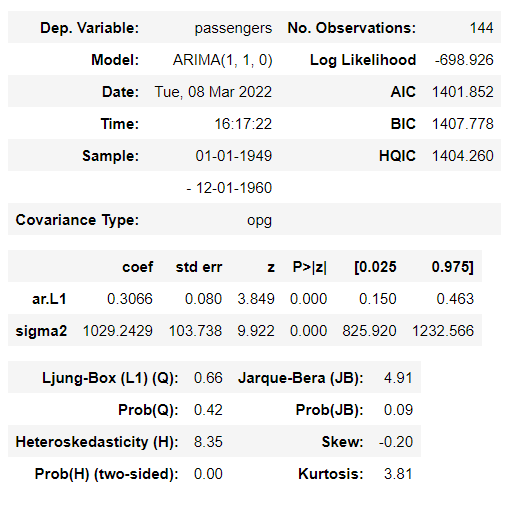

위와 같은 결과를 얻을 수 있다. order 이 1,1,0 이라는 의미는 한번 차분이후 p=1 q=0이라는 의미이고

Yt = 0.3Yt-1 + e 

이런 모형이고 sigma2는 e잔차의 분산값이다.

def forecast_plot(data, fit, num):
    try:
        pred = fit.get_forecast(num)

        pred_val = pred.predicted_mean
        pred_lb = pred.conf_int().iloc[:,0]
        pred_ub = pred.conf_int().iloc[:,1]
        pred_index = pred_ub.index
    except:
        arima_res = ARIMA(airDF, order=(1, 0, 0)).fit()
        pred22 = arima_res.get_forecast(num)
        pred_index = pred22.predicted_mean.index
        
        pred = fit.predict(num, return_conf_int =True)

        pred_val = pred[0]
        pred_lb = pred[1][:,0]
        pred_ub = pred[1][:,1]
    fig, axes= plt.subplots(figsize = (10, 4))
    axes.plot(data)
    axes.vlines(pred_index[0],0,700, linestyle='--', color = 'red')
    axes.plot(pred_index,pred_val, label ='predict')
    axes.fill_between(pred_index, pred_lb, pred_ub, color ='k', alpha=0.1, label='0.95 interval')
    plt.title('prediction')
    plt.show()
    
forecast_plot(airDF,arima_res,12)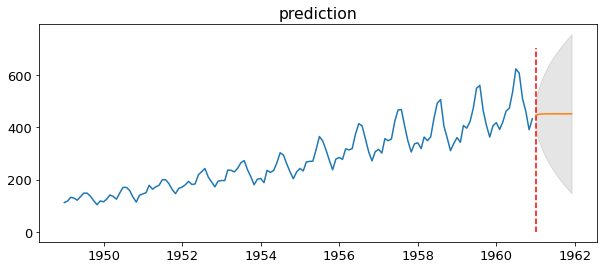

주황값이 예측값이다.

위의 데이터는 계절성이 있지만 위 arima모델로는 계절성을 설명하지 못하기때문에 옳지 못하다. 그렇기에 후에 Sariama모델을 설명핟겓.

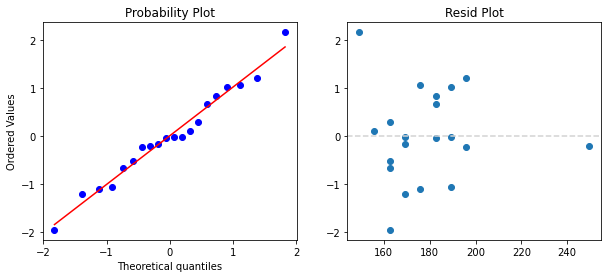
arima_res.plot_diagnostics()
plt.show()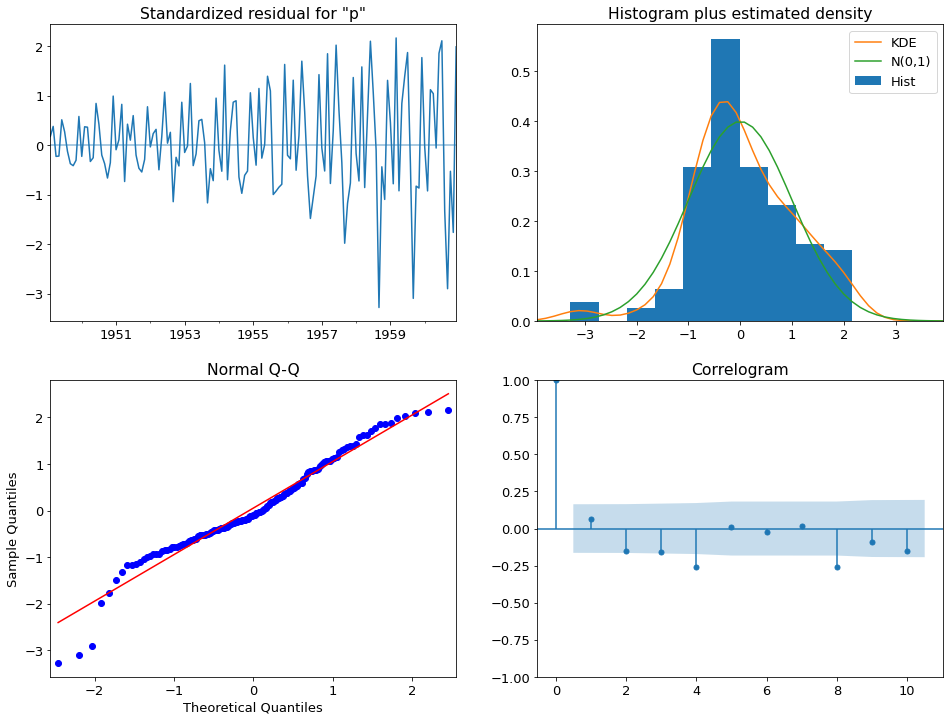

원하는 결과가 나왔다면 백색잡음과정의 ㄱ가정을 몇가지 확인하게 된다.

E(Xt) = 0

Var(Xt) = sigma^2 (all t)

Cov(Xt, Xs) = 0  (t!=s)

정규분포의 갖어과 비슷하지만 iid의 가정이 빠진경우이다.

위가정이 만족하는지 보여주는 그래프들을 보며 가정이 맞는지 확인한다.

하지만 좌측상단의 그래프를 보면 분산이 t가 커짐에 따라 커지는 것을 확인할 수 있기때문의 위의 적합은 옳지 않다고 할 수 있다.

from statsmodels.tsa.statespace.sarimax import SARIMAX

sarima_res = SARIMAX(airDF, order=(1, 1, 0), seasonal_order = (1,1,2,12)).fit()
sarima_res.summary()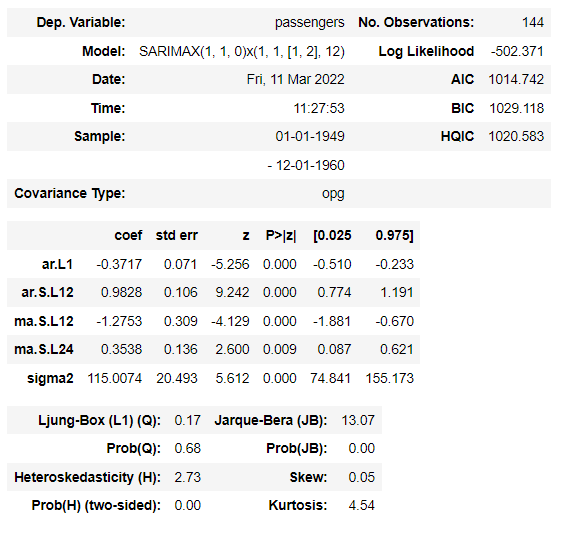

계절성의 주기가 12라는 뜻이다.  seasonal_order은 계절차수이다.

forecast_plot(airDF,sarima_res,12)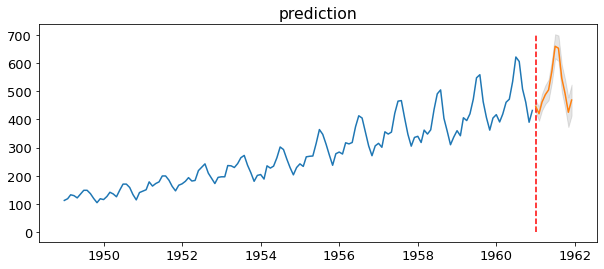

이상적이어 보인다.

sarima_res.plot_diagnostics()
plt.show()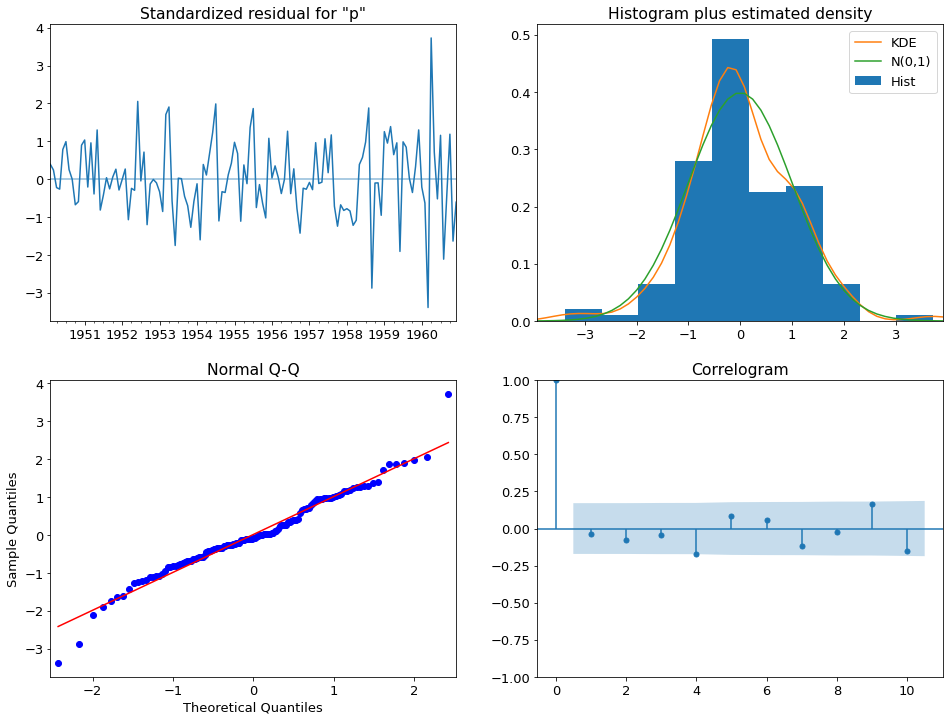

가정이 아주 잘 만족하는 것으로 보인다.

from pmdarima.arima import auto_arima

auto_arima_result = auto_arima(airDF, start_p = 1, start_q = 1, max_p = 3, max_q = 3,
          seasonal = True, d = 1, D=1, m=12, start_P = 1, start_Q = 1, max_P = 3, max_Q = 3, trace=True,
          error_action = 'ignore', suppress_warnings = True, stepwise=False)

원래는 차분을 반복하며 어떤 차수가 맞는지 반복하고 acf,pacf에 맞추어 p와 q를 맞추는 과정이 필요하지만

위의 모듈을 사용하면 자동적으로 aic가 낮은 녀석을 선택해준다.

위의 가정을 확인하는 함수나 예측시각화 그래프, summary 또한 그대로 적용가능하다

각 개체에 대한 결과를 1 이나 0으로 나타내는 이항반응변수에 대하여 설명

성공할 확률을 나타냄

반응변수가 범주형변수인 경우 선형회귀분석은 적합치않음

1. 로지스틱회귀모형

로지스틱회귀모형은 확률의 로직, 즉 오즈의 로그갑에 대해 다음 같은 선형식을 가정한다.

1) 오즈 

오즈 (odds) & 로짓 변환성공 확률이 실패 확률에 비해 몇 배 더 높은가를 나타내며 그 식은 아래와 같다.

예를 들어 성공확률이 0.8이라면 0.8/1-0.8 = 4 로 성공확률이 실패확률보다 4배 높다는 것을 의미함

2) 로짓변환

로짓 변환오즈에 로그를 취한 함수

오즈의 경우 실패확률이 아무리 커도 0에 가까운 반면 성공확률이 아주 클경우에는 무한대에 가깝게 된다.

그래서 서로 대칭을 맞추어 주기위해서 로그를 붙여준다

로그변환을 하면 0을 기준으로 대칭한다. 

3) 로지스틱함수

로지스틱 함수의 그래프는 Figure 1과 같고 이는 독립 변수 x가 주어졌을 때 종속 변수가 1의 범주에 속할 확률을 의미한다. 즉, p(y=1|x) 를 의미한다.로지스틱 함수는 로짓

변환을 통해 만들어지고, 그 형태는 다음과 같다.

(출처) 위키백과

로지스틱함수는 우측 그래프같이 s자 모양을 띈다.

일반 회귀분석의 경우에는 기울기가 일정하지만 로지스틱함수는 기울기가 일정하지 않은 모습을 볼 수 있다.

2. 실습 

데이터

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

from statsmodels.formula.api import logit

crabs = pd.read_csv('crabs.csv')
crabs.head()

y값이 반응변수인 것  암컷이 부수체를 가지냐(1) 아니냐(0)

등딱지의 너비 width

model = logit('y~width', data =crabs).fit()

sns.scatterplot(x = 'width',y = 'y', data = crabs)
x_ = np.arange(crabs['width'].min(),crabs['width'].max(),0.01)
y_ = model.predict({'width':x_})
sns.lineplot(x = x_, y = y_, color = 'red')
plt.show()

model.summary()

상단의 

로지스틱 회귀모형은 x가 1증가할 때 여기서는 (width) 로짓이 beta만큼 증가하는 것을 나타낸다

위 결과로부터 로지스틱회귀모형을 적합하면

logit( pi(x) ) = -12.35(alpha) + 0.497*width(beta)  이다. 

이를 정리하면

pi(x)  =  exp(-12.35 + 0.497 * width) / 1 + exp(-12.35 + 0.497 * width)  이다.

beta > 0 이기 때문에 너비값이 커지면 예측확률 은 커진다.

만약 여러가지의 독립변수들이 있었다면 우측의 p > |z| 값을 확인하면서 해당 변수가 종속변수의 변화에 유의한가를 확인 할 수 있다. 

위의 width는 아주 유의한 것으로 확인된다. 

model.predict({'width':21})

0    0.129096
dtype: float64

너비가 21 일 때의 부수체가 있을 확률은 0.129가된다.

혼동행렬

model.pred_table()

array([[27., 35.],
       [16., 95.]])

모형의 적합도 판단

model.aic

198.45266392876505

단순선형회귀분석

선형적인 관계에 있는 독립변수와 종속변수의 관계를 하나의 1차식으로 도출하여 일반화 하는 방법

회귀분석은 종속변수에 미치는 독립변수의 영향파악이며 독립변숭가 변화할때 종속변수가 어느정도가 될지 예측하는 목적

엄밀하게 말하면 인과관계가 성립하려면

1. 시간의 선후차성

2. 비허위적관계

두가지가 충족되어야함

실습

데이터 

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

from scipy import stats

from sklearn.datasets import load_linnerud

linnerud = load_linnerud()
linnerud_data = np.concatenate((linnerud['target'], linnerud['data']),axis=1)
linnerud_columns = linnerud['target_names'] + linnerud['feature_names']

df = pd.DataFrame(linnerud_data, columns = linnerud_columns)
df.head()

ax = sns.regplot(x='Waist', y='Weight', data=df)

기본적으로 선형성을 띄는지 확인하는게 좋음

적합

from statsmodels.formula.api import ols 

model = ols('Weight ~ Waist', data = df)
fit = model.fit()
fit.summary()

상단의 표부터 좌상단에서 부터 설명

1. No. Observations: 데이터의 수

2. Df Residuals : 잔차의 자유도 n - df model -1

3. Df Model : 모델의 자유도 설명변수의 갯수

4. R-squared : 결정계수 

결정계수 = ssr (회귀식으로 설명되는 변동) / sst (전체변동)

sst = sse + ssr

전체 변동에서 회귀식으로 설명되는 변동의 정도 -> 높으면 모델의 설명력이 크다

5. Adj. R-squared : 수정된 결정계수

결정계수에서 변수의 갯수와 데이터의 갯수를 고려하여 보정한 값

일반 결정계수는 의미가 없는 설명변수라도 추가된다면 무조건 결정계수가 올라가기에 그 단점을 보완한 것 모델간의 비교에는 이 녀석이 좋음

Intercept : 절편

그 아래 행 : 각 변수

1. coef : 계수

intercept의 경우 : 독립변수가 0일때 종속변수는?

독립변수의 경우 : 독립변수가 1증가할때 종속변수가 얼마나 변화하냐

2. std err : 표준편차

예측한 coef에 대한 표준편차

3. t : 계수 추정에 대한 tvalue 비교는 0이랑 비교 coef / std err 값과 같음 빼는 놈이 0이라서

4. P > |t| : 귀무가설 : beta = 0 라는 가설에 대한 p value 0에 가까울수록 0이 아니다라는 의미 (즉 의미가 있다, 유의하다)

1. Durbin-Watson: 더빗왓슨 검정값 2에 가까울 수록 잔차의 자기 상관이 없ㅇㅇㅁ

2보다 작고 0에 가까우면 양의 자기상관 2보다크고 4에가까우면 음의상관

모형진단

def resid_test(fit):
    resid = fit.resid / np.sqrt(fit.mse_resid) # 스튜던트화잔차
    fig, axes= plt.subplots(1,2, figsize = (10, 4))
    stats.probplot(resid, dist=stats.norm, plot = axes[0])
    axes[1].plot(fit.fittedvalues, resid, 'o')
    axes[1].axhline(0, color='lightgray', linestyle='--', linewidth=1.5)
    axes[1].set_title("Resid Plot")
    plt.show()
    
resid_test(fit)

회귀분석의 가정 만족하는지 확인

1. 선형성, 2. 오차의 독립성, 3.오차의 등분산성

우측 잔차 산점도로 잔차 산점도가 특이한 패턴을 가지지않는다면 만족

4. 오차항의 정규성 좌측 qq plot으로 

5. 오차항의 독립성 위 적합결과에서 더빈왓슨 검정값 확인

영향점분석

def plot_influence(fit):
    influence = fit.get_influence()
    cook_plot = influence.plot_index()
    influ_plot = influence.plot_influence()
    plt.show()
plot_influence(fit)

각 관측값이 얼마나 적합값과 거리가 큰가를 확인할 수 있는 cook의 거리와 버블차트 8번데이터가 예측값과 실제값이 차이가 큼 

큰녀석들을 뺴고 다시 적합한다면 더 일반화된 결과를 얻을 수 있을 것 (더 높은 결정계수)

예측

print('fited value')
display(fit.fittedvalues.head(2))
print('residuals')
display(fit.resid.head(2))
print('prediction')
print(fit.predict({'Waist':[50,60],'Pulse':[10,20]}))

fited value
0    182.626283
1    189.336756
dtype: float64
residuals
0    8.373717
1   -0.336756
dtype: float64
prediction
0    276.572895
1    343.677618
dtype: float64

각각 적합값, 잔차, 예측방법

독립변수항에 더 추가하면 여러가지 독립변수로 가능

1. 상관관계

2개의 변량 x와 y사이에 한쪽 변화가 다른 한쪽의 변화에 어떤 영향을 주는 경향이 있을 때 x와 y의 사이에는  상관관계(correlation)이 있다고 한다.

2. 상관계수 

두변량 x와 yt사이에 직선적인 상관관계의 정보를 표본으로 부터 얻은 값을 표본상관계수라고한다.

3. 상관계수의 성질

1) -1 <= r <= 1 

2) 상관이 없으면 r=0

3) 양수이면 한 변수가 증가하면 다른 변수도 증가하는 관계 음수면 한 변량이 증가하면 다른 변수는 감소하는 관계

4. 실습

실습데이터 

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

from scipy import stats

from sklearn.datasets import load_linnerud

linnerud = load_linnerud()
linnerud_data = np.concatenate((linnerud['target'], linnerud['data']),axis=1)
linnerud_columns = linnerud['target_names'] + linnerud['feature_names']

df = pd.DataFrame(linnerud_data, columns = linnerud_columns)
df.head()

사이킷런에서 제공하는 몸무게, 허리둘레,혈압, + 운동능력 데이터를 사용

상관행렬 

def corr_heat(df):
    plt.figure(figsize=(7,7))

    corr_df = df.corr()
    display(corr_df)

    mask = np.zeros_like(heat_table)
    mask[np.triu_indices_from(mask)] = 1
    heat_map = sns.heatmap(corr_df, annot=True, mask = mask, cmap='coolwarm')
    heat_map.set_xticklabels(heat_map.get_xticklabels(), fontsize=12, rotation=45)
    heat_map.set_yticklabels(heat_map.get_yticklabels(), fontsize=12)
    plt.title('corr between features', fontsize=15)
    plt.show()
    
corr_heat(df)

pandas의 corr을 이용해서 두변수간의 상관계수를 확인 가능하다.

대각원소는 같은 변수끼리의 상관계수이기 때문에 당연히 1이고 대각원소를 기준으로 대칭이기에 표현x

몸무게와 허리둘레가 양의 상관관계를 보인다.

pair plot

plt.figure(figsize=(7,7))
sns.pairplot(df, diag_kind='hist')

각 변수들끼리의 산점도

두 변수의 상관분석

def corr_two(col1,col2,df):
    sns.jointplot(col1, col2, data=df)
    plt.show()
    col_1 = df[col1]
    col_2 = df[col2]
    p_test = stats.pearsonr(col_1,col_2)
    print('*** pearson-corr-test *** \n corr = %6.3f pvalue = %6.4f\n' % p_test)

corr_two('Waist','Weight',df)

상관계수가 0인지 아닌지 검정가능 

귀무가설 : 두 변수의 상관계수는 0이다

대립가설 : 두 변수의 상관계수는 0이아니다.

1. ANOVA란?

ANalysis Of VAriance의 약자로 한국말로 직역하면 분산분석이다.

anova는 2개이상의 그룹의 평균을 비교하는 방법이다.

정규분포로부터 생성한 다음 예를 활용해서 설명을 지속하겠다.

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

from scipy import stats

rvs1 = np.random.normal(1,1,100)
rvs2 = np.random.normal(3,1,100)
rvs3 = np.random.normal(5,1,100)

mean1, std1, size1 = np.mean(rvs1), np.std(rvs1), len(rvs1)
print(f'data1  mean : {mean1:0.2f}, std: {std1:0.2f}, size : {size1}')
mean2, std2, size2 = np.mean(rvs2), np.std(rvs2), len(rvs2)
print(f'data2  mean : {mean2:0.2f}, std: {std2:0.2f}, size : {size2}')
mean3, std3, size3 = np.mean(rvs3), np.std(rvs3), len(rvs3)
print(f'data2  mean : {mean3:0.2f}, std: {std3:0.2f}, size : {size3}')


plt.figure(figsize = (10, 5))
sns.kdeplot(data = rvs1, color = 'red', shade = True)
sns.kdeplot(data = rvs2, color = 'blue', shade = True)
sns.kdeplot(data = rvs3, color = 'green', shade = True)
plt.show()

data1  mean : 0.81, std: 1.01, size : 100
data2  mean : 3.09, std: 0.96, size : 100
data2  mean : 4.92, std: 1.04, size : 100

rvs_total =np.concatenate((rvs1, rvs2, rvs3))
plt.figure(figsize = (10, 5))
sns.kdeplot(data = rvs_total, color = 'purple', shade = True)
plt.show()

2번그래프를 보면 하나의 집단이지만 각각 다른 수준으로 보면 1번그래프의 모양을 띈다.

anova는 이러한 그룹간의 평균을 비교하여 통계적으로 그룹끼리 다른지 유사한지 알아내기를 도와준다.

anova의 결과는 f통계량이다.

정규분포를 제곱하면 chisq분포가 된다. 정규분포는 평균을 추정하는데 사용하고 평균에 제곱이 들어가는 다른 통계값은 분산이다. 정규분포를 제곱한 chisq분포는 분산을 추정하는데에 사용한다.

F분포는 두가지의 chisq분포를 분자와 분모로 나눈 값이다.

다시말하면 분산의 비를 추정할 수 있는 분포이다.

anova에서는 집단간의 분산 / 집단내의 분산 으로 집단간의 이질성을 검정한다.

집단 내의 동질성이 늘어나고 집단간의 분산이 커지면  F통계량은 커질것이며 이것은 귀무가설을 강하게 반하는 결과를 가져오게된다.

귀무가설(H0) : 그룹이나 평균 간에 차이가 없다.

대립가설(H1) : 집단의 평균 사이에 차이가 있다.

2. 분산분석의 가정

• 독립성: 한 관측치에 대한 종속 변수 값은 다른 관측치 값과 독립
• 종속 변수의 값이 정규 분포를 따릅니다.
• 등분산성 
• 종속 변수는 연속적.

저번 포스팅에서 사용했던 levene_test와 norm_test를 그대로 사용해서 각각 확인하면된다.

https://gwoolab.tistory.com/39

3. 분산분석의 종류와 실습

- 일원배치분산분석

scipy 이용

anova_one = stats.f_oneway(rvs1, rvs2, rvs3)

print('oneway anova F-statistic = %6.3f pvalue = %6.4f' % anova_one )

oneway anova F-statistic = 354.784 pvalue = 0.0000

pvalue가 0에 가까운 값이기에 귀무가설을 기각한다. 즉 최소 한가지에 그룹이 다른 그룹의 평균과는 다르다

statsmodel 이용

import statsmodels.api as sm 
from statsmodels.formula.api import ols 

model = ols('value ~ C(group)', data=anova_df).fit() 
sm.stats.anova_lm(model, typ=1)

statsmodel은 좀 더 자세한 결과를 보여줍니다.

연산의 결과는 같음

위의 결과에 따르면 그룹에 따라 값이 영향을 받는다고 할 수 있다.

- 이원배치분산분석

penguin = sns.load_dataset('penguins')
penguin = penguin[['species','sex','body_mass_g']].dropna()
penguin.head()

펭귄의 종과 성별에 따라서 몸무게가 영향을 받는지를 검정하고자한다.

model = ols('body_mass_g ~ C(species)+C(sex)+C(species):C(sex)', penguin).fit()
result = sm.stats.anova_lm(model, typ=1)

pd.options.display.float_format = '{:,.4f}'.format
# pd.options.display.float_format = '{:.2e}'.format

result

formula 부분에서 C(species):C(sex)는 두 변수의 교호작용을 의미한다.

모든 pvalue와 F값이 귀무가설을 기각하고 있다.

즉 펭귄의 종, 펭귄의 성별에 따라서 펭귄의 몸무게 차이가 유의하다 즉 영향을 준다라고 할 수 있고

교호작용 텀도 유의한 것으로 보아 종이 몸무게에 미치는 영향력의 크기가 성별에 따라서 달랒 질 수 있다는 것을 의미한다

4. etc

ANOVA는 최소 두 그룹의 평균 간에 유의한 차이가 있는지 여부만 알 수 있지만 평균이 다른 쌍은 설명할 수 없다. 세

데이터가 정규 곡선에 분포하지 않고 이상값이 있는 경우 검정의 결론이 부정확할 수 있다.

표준편차의 차이가 크면 검정의 결론이 부정확할 수 있다.

ANOVA는 모델의 복잡성을 줄이기 위해 입력 변수의 수를 최소화한다.

ANOVA는 독립 변수가 대상 변수에 영향을 미치는지 여부를 결정하는 데 도움이 된다.

또한 그룹간의 평균이 다른지 아닌지만을 아렬주고 어떤 그룹의 평균이 큰지에 대한 내용은 제공하지않기때문에 

사후분석이 수반되기도한다.

1. T-분포란

- 표본평균으로 정규분포를 따르는 모집단의 평균을 해석할 때 사용

- 모집단의 분산이 알려져 있지 않은 경우에 정규분포 대신 이용하는 확률분포

- 정규분포 보다 두꺼운 꼬리

- 일반적으로 n이 30이상이면 중심극한정리에 의해 정규분포로 취급한다.

2. T- test의 가정

t-test는 종류마다 각각의 가정을 가지지만 공통적으로 적용되는 것이 있다.

표본이 정규성을 띄느냐 인데 t분포라고 가정을 하고 들어가기때문에 t분포라고 가정할 수 있느냐를 정규성검정으로 확인하는 과정이라고 할 수 있다. (t분포 자체가 정규분포에서 나온 것이기 때문에)

- 정규성검정

실습을 위한 데이터 생성

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

from scipy import stats


rvs1 = np.random.normal(10,1,100)
rvs2 = np.random.normal(11,1,100)

mean1, std1, size1 = np.mean(rvs1), np.std(rvs1), len(rvs1)
print(f'data1  mean : {mean1:0.2f}, std: {std1:0.2f}, size : {size1}')
mean2, std2, size2 = np.mean(rvs2), np.std(rvs2), len(rvs2)
print(f'data2  mean : {mean2:0.2f}, std: {std2:0.2f}, size : {size2}')

plt.figure(figsize = (10, 5))
sns.kdeplot(data = rvs1, color = 'red', shade = True)
sns.kdeplot(data = rvs2, color = 'blue', shade = True)
plt.show()

data1  mean : 10.09, std: 0.99, size : 100
data2  mean : 10.98, std: 0.96, size : 100

rvs1은 평균이 10 표준편차가 1인 정규분포에서 100개를 샘플링한값

rvs2은 평균이 11 표준편차가 1인 정규분포에서 100개를 샘플링한값 이다.

정규성검정

def norm_test(dist):
    fig, axes= plt.subplots(1,2)
    plt.figure(figsize = (7, 7))
    stats.probplot(dist, dist=stats.norm, plot = axes[0])
    sns.distplot(dist, ax=axes[1])
    plt.show()
    
    print('null hypothesis : Data is a normal distribution.\n')
    
    len_ = len(dist)
    ks_dist = dist - np.mean(dist)
    ks_test = stats.kstest(ks_dist,'norm', N = len_)
    print('*** Kolmogorov-Smirnov test *** \n t-statistic = %6.3f pvalue = %6.4f\n' % ks_test)

    shapiro_test = stats.shapiro(dist)
    print('*** shapiro-Wilk test *** \n t-statistic = %6.3f pvalue = %6.4f' % shapiro_test)
    
    
    
 norm_test(rvs1)

null hypothesis : Data is a normal distribution.

*** Kolmogorov-Smirnov test *** 
 t-statistic =  0.048 pvalue = 0.9688

*** shapiro-Wilk test *** 
 t-statistic =  0.992 pvalue = 0.8079

좌측에 보이는 그래프는 R에서 사용했던 노말qq플롯이다 좌하단과 우상단의 모서리를 잇는 빨간대각선에 비슷하게 파란점들이 위치하면 정규성을 띈다고 할 수 있다.

Kolmogorov-Smirnov test와 shapiro-Wilk test 모두 정규성을 검정하는 통계적 방법인데

두 검증 모두 데이터가 정규성을 띈다라는 귀무가설을 가지고 있다.

보통쓰이는 유의수준인 0.05를 적용한다면 두 테스트의 결과 모두 귀무가설을 기각할 충분한 근거가 없다.

즉 정규성을 만족한다.

3. T -test의 종류 및 실습

- 일표본 t검정 one sample T-test

one_sample_ttest = stats.ttest_1samp(rvs1, 10, axis=0,  alternative='two-sided')
print('one sample t-statistic = %6.3f pvalue = %6.4f' % one_sample_ttest )

one sample t-statistic = -0.597 pvalue = 0.5516

stats.ttest_1samp(데이터, mu1, axis=0,  alternative='two-sided')

alternative : 'two-sided', 'less', 'greater' 중 선택 (대립가설)

rvs1이라는 데이터의 모평균이 10이아니다 라는 대립가설에 대한 가설 검정을 실시한 코드이다.

p-value가 0.55로 모평균이 10이라는 귀무가설을 기각할 충분한 근거가 없다는 검정 결과이다.

즉 모평균이 10일것이라고 말하고 있다.

단측검정을 실시한다면 alternative의 옵션을 달리하면된다.

less로 설정한다면 대립가설은 mu < mu1

greater로 설정한다면 대립가설은 mu > mu1

가 될 것이다.

- two sample t-test

두 데이터의 평균차에 대한 검정입니다. 

먼저 두 데이터의 분산이 같은지(통계적으로 비슷한지)에 따라서 검정을 수행할 때의 수식이 달라지기 때문에 (합동 표본표준편차를 이용한다거나)

등분산 검정을 먼저 실시하고 어떤 옵션으로 실시할지를 결정한다.

levene_test = stats.levene(rvs1, rvs2)
print('null hypothesis : populations have equal variances.')
print('levene test t-statistic = %6.3f pvalue = %6.4f' % levene_test )

null hypothesis : populations have equal variances.
levene test t-statistic =  0.007 pvalue = 0.9342

levene_test는 두 데이터의 등분산성을 검정하는 검정이고 귀무가설은 두데이터가 등분산성을 띈다이다.

pvalue가 0.05보다 높기때문에 두 데이터는 등분산성을 띈다고 할 수 있다.

  - 등분산의 경우

var_equal_ttest = stats.ttest_ind(rvs1,rvs2, equal_var = True, alternative = 'two-sided')
print('variance equal t-statistic = %6.3f pvalue = %6.4f' % var_equal_ttest )

variance equal t-statistic = -6.433 pvalue = 0.0000

pvalue가 아주 작은 수준이므로 귀무가설은 기각한다. 즉 두 모평균은 다르다

- 이분산의 경우

non_equal_ttest = stats.ttest_ind(rvs1,rvs2, equal_var = False, alternative = 'two-sided')
print('non equal t-statistic = %6.3f pvalue = %6.4f' % non_equal_ttest )

등분산 검정에서 서로 분산이 다르다는 검정결과가 나왔을 경우 위 코드를 활요하면된다.

만약 이표본 데이터 검정시 두평균이 같은지가 아니라 평균이 a만큼 차이난다를 검중하고 싶다면 한 데이터에 상수 a를 더하면 수행이 가능하다.

두 모평균의 차이가 1일 것이라는 귀무가설을 기각하지 못한다.

실제로 두 모평균의 차이는 1이었다.

대립가설의 옵션은 일표본ttest와 같은 방법으로 적용된다.

  - paired T-test 

순서별로 쌍을 이룬 데이터로 고려하여 두 데이터의 평균차를 검정한다.

실제 예를 든다면 

 동일한 피실험자들에 대한 처치 이전 이후를 확인하는 경우이다.

다이어트 약의 효과를 보기 위해 먹기전의 몸무게 먹은후의 몸무게가 이 예가 될 수 있겠다. 물론 다른 조건은 동일하게 줘야한다.

bias = np.random.normal(1,1,100)
bias[np.where(bias<0)] = 0
rvs1_bias = rvs1 + bias

non_equal_ttest = stats.ttest_rel(rvs1,rvs1_bias)
print('paired t-statistic = %6.3f pvalue = %6.4f' % non_equal_ttest )

paired t-statistic = -11.551 pvalue = 0.0000

rvs1에 양수 or 0을 더한 값을 처치 이후로 가정하고 검정을 실시하였다.

pvalue가 아주 작은 값을 가지기때문에 처치이전과 이후의 모평균에는 유의미한 차이가 있다고 할 수 있다.

이 경우에도 대립가설의 수정과 a만큼의 차이는 위의 이표본,일표본의 경우와 같게 적용 가능하다.

통계를 공부하면서 모평균 추정 등 여러가지 추정을 하게된다.

여러가지 가설검정을 파이썬으로 검정하는 방법을 포스팅하기 전에 가설검정이란 무엇인가를 정리하고자 한다.

통꼐에서는 기본적으로 전수조사가 되지 않기때문에 

샘플링이 필수적으로 들어가게된다.

일반적 수학적증명과는 다른 점이 있다. 

수학적증명은 100% 이지만

통계적증명은 100% 확신할 수 없다.

그래서 신뢰도라는 말이 따라 붙는 것이다 통계적 가설은 언제나 틀렸을 확률을 내포한다.

귀무가설 null hypothesis (H1) : 대립가설에 반대되는 가설

대립가설 alternative hypothesis(H0) : 모집단에 대하 새롭게 제기된 이론이나 주장 -> 표본을 통해 입증하고자 하는 가설

표본을 통해 대립가설을 지지할 통계적증거가 있는지를 확인하는 과정을 가설검정이라고 한다.

1. 가설

α = P(H0 reject |H0 true)

1종 오류를 범할 확률 알파 : 귀무가설이 사실인데 귀무가설을 기각시키는경우 = 유의수준

β = P(H0 accept |H0 false)

2종 귀무가설이 거짓인데 귀무각설을 채택하는 경우

좋은 가설검정이란 이 두가지 오류가 일어날 확률을 최소화는 것이다.

일반적으로 두종류의 오류는 반비례관계여서 둘다 줄이기는 쉽지않다.

보통 1종 오류를 범했을떄 큰손실이 발생하는 경우가 많기 때문에 alpha를 줄이는 방향으로 하는 것이 옳다.

그의 예로 가장 많이 드는 문제는 신약의 문제이다. 어떤 회사가 신약을 개발한다고 했을 때

H0 : 기존약과 신약이 차이가 없다.

H1 : 신약이 기존약보다 더 좋다.

위의 가설이 있다고라면 

제 1종 오류 : 별차이가 없어도 신약추진

제 2종 오류 : 신약이 효과가 있음에도 개발을 안함

1종 오류를 범했을 때 회사의 입장에서 손실이 생긴다는 것이다.

보통 1종 오류의 최대 허용한계(유의수준) (0.01,0.05,0.1)를 정해놓고 그 안에서

제 2종 오류를 최소화해주는 방법으로 가설을 검정하게된다.

가설 검정을 위해서는 보통 모집단의 분포를 추론하게 된다.

2. p-value

p-value : 귀무가설에서 주장한 바가 옳을 확률

 예를 들어

H0 : mu = 95 

H1 : mu >95

모평균이 95이다라는 가설하에 샘플링한 데이터의 평균이 120, 표준편차가 5일 경우 

평균이 95인 모집단에서 본다면 우연이 여러번 발생한 것이다.

우연이 여러번발생했다면 처음에 생각했던 가설이 아닐 수 있다는 것이다.

만약 낙제생이라고 평가했던 학생 A가 열 번의 시험에서  100점을 받는경우 사실 저 학생은 낙제생이 아닐 것이라고 생각하는 논지와 같다.

우연히 발생할 가능성이 매우 희박한 사건이 실제로 발생했을 경우, 그것은 우연이 아니라고 생각하는 경향이 있고,

p-value 역시 그와 같은 개념이라고 할 수 있다.

위의 예로 말하면 실제로 모평균이 95인 모집단에서 평균이 120인 샘플링을 할 확률이 p-value인 것이다. 낮으면 가설이 틀렸을거다 높으면 그렇게 나올만 하다 이렇게 되는 거다.

두번째 예로는 A 가 열 번의 시험에서 우연히 100점을 맞을 확률이 p-value이다. 확률이 낮다면 사실 A는 낙제생이 아닐 거야라고 말하는 것이다.

p-value가 낮으면 귀무가설이 틀렸다는 말이라고 할 수 있다.

0.05이상이라면 아마 우연으로 나온것일 것이다.

0.05이하이면 우연이 아닐 수도 있을 것이다.

귀무가설이 맞을 수도있다.-> 대립가설이 맞다고하지 못한다 -> 귀무가설을 기각하지 못한다.

위의 개념을 적용하면서 확률을 추정하기 위해서 보통 모집단이 어떤 분포를 따를 것이라고 하고 시작한다. 그래서 가설검정에 앞서 어떤 분포를 따르는지 확정짓는것이 중요ㅕ하다.

통계에서는 확신에 찬 말을 해서는 안된다.