단순선형회귀분석
선형적인 관계에 있는 독립변수와 종속변수의 관계를 하나의 1차식으로 도출하여 일반화 하는 방법
회귀분석은 종속변수에 미치는 독립변수의 영향파악이며 독립변숭가 변화할때 종속변수가 어느정도가 될지 예측하는 목적
엄밀하게 말하면 인과관계가 성립하려면
1. 시간의 선후차성
2. 비허위적관계
두가지가 충족되어야함
실습
데이터
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from scipy import stats
from sklearn.datasets import load_linnerud
linnerud = load_linnerud()
linnerud_data = np.concatenate((linnerud['target'], linnerud['data']),axis=1)
linnerud_columns = linnerud['target_names'] + linnerud['feature_names']
df = pd.DataFrame(linnerud_data, columns = linnerud_columns)
df.head()| Weight | Waist | Pulse | Chins | Situps | Jumps | |
| 0 | 191.0 | 36.0 | 50.0 | 5.0 | 162.0 | 60.0 |
| 1 | 189.0 | 37.0 | 52.0 | 2.0 | 110.0 | 60.0 |
| 2 | 193.0 | 38.0 | 58.0 | 12.0 | 101.0 | 101.0 |
| 3 | 162.0 | 35.0 | 62.0 | 12.0 | 105.0 | 37.0 |
| 4 | 189.0 | 35.0 | 46.0 | 13.0 | 155.0 | 58.0 |
ax = sns.regplot(x='Waist', y='Weight', data=df)
기본적으로 선형성을 띄는지 확인하는게 좋음
적합
from statsmodels.formula.api import ols
model = ols('Weight ~ Waist', data = df)
fit = model.fit()
fit.summary()상단의 표부터 좌상단에서 부터 설명

1. No. Observations: 데이터의 수
2. Df Residuals : 잔차의 자유도 n - df model -1
3. Df Model : 모델의 자유도 설명변수의 갯수
4. R-squared : 결정계수
결정계수 = ssr (회귀식으로 설명되는 변동) / sst (전체변동)
sst = sse + ssr
전체 변동에서 회귀식으로 설명되는 변동의 정도 -> 높으면 모델의 설명력이 크다
5. Adj. R-squared : 수정된 결정계수
결정계수에서 변수의 갯수와 데이터의 갯수를 고려하여 보정한 값
일반 결정계수는 의미가 없는 설명변수라도 추가된다면 무조건 결정계수가 올라가기에 그 단점을 보완한 것 모델간의 비교에는 이 녀석이 좋음

Intercept : 절편
그 아래 행 : 각 변수
1. coef : 계수
intercept의 경우 : 독립변수가 0일때 종속변수는?
독립변수의 경우 : 독립변수가 1증가할때 종속변수가 얼마나 변화하냐
2. std err : 표준편차
예측한 coef에 대한 표준편차
3. t : 계수 추정에 대한 tvalue 비교는 0이랑 비교 coef / std err 값과 같음 빼는 놈이 0이라서
4. P > |t| : 귀무가설 : beta = 0 라는 가설에 대한 p value 0에 가까울수록 0이 아니다라는 의미 (즉 의미가 있다, 유의하다)

1. Durbin-Watson: 더빗왓슨 검정값 2에 가까울 수록 잔차의 자기 상관이 없ㅇㅇㅁ
2보다 작고 0에 가까우면 양의 자기상관 2보다크고 4에가까우면 음의상관
모형진단
def resid_test(fit):
resid = fit.resid / np.sqrt(fit.mse_resid) # 스튜던트화잔차
fig, axes= plt.subplots(1,2, figsize = (10, 4))
stats.probplot(resid, dist=stats.norm, plot = axes[0])
axes[1].plot(fit.fittedvalues, resid, 'o')
axes[1].axhline(0, color='lightgray', linestyle='--', linewidth=1.5)
axes[1].set_title("Resid Plot")
plt.show()
resid_test(fit)
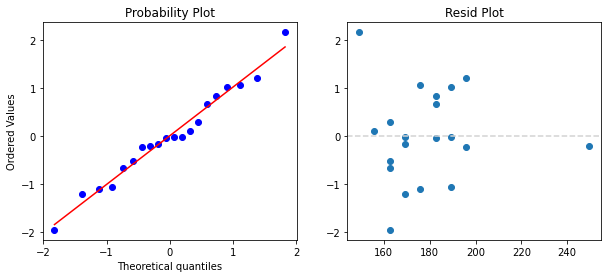
회귀분석의 가정 만족하는지 확인
1. 선형성, 2. 오차의 독립성, 3.오차의 등분산성
우측 잔차 산점도로 잔차 산점도가 특이한 패턴을 가지지않는다면 만족
4. 오차항의 정규성 좌측 qq plot으로
5. 오차항의 독립성 위 적합결과에서 더빈왓슨 검정값 확인
영향점분석
def plot_influence(fit):
influence = fit.get_influence()
cook_plot = influence.plot_index()
influ_plot = influence.plot_influence()
plt.show()
plot_influence(fit)

각 관측값이 얼마나 적합값과 거리가 큰가를 확인할 수 있는 cook의 거리와 버블차트 8번데이터가 예측값과 실제값이 차이가 큼
큰녀석들을 뺴고 다시 적합한다면 더 일반화된 결과를 얻을 수 있을 것 (더 높은 결정계수)
예측
print('fited value')
display(fit.fittedvalues.head(2))
print('residuals')
display(fit.resid.head(2))
print('prediction')
print(fit.predict({'Waist':[50,60],'Pulse':[10,20]}))fited value
0 182.626283
1 189.336756
dtype: float64
residuals
0 8.373717
1 -0.336756
dtype: float64
prediction
0 276.572895
1 343.677618
dtype: float64각각 적합값, 잔차, 예측방법
독립변수항에 더 추가하면 여러가지 독립변수로 가능
'통계' 카테고리의 다른 글
| [통계] 시계열 분석, 분해법, arima (0) | 2022.03.11 |
|---|---|
| [통계] 로지스틱 회귀분석 (0) | 2022.03.10 |
| [통계] 상관분석 (0) | 2022.03.03 |
| [통계] ANOVA 분산분석 (0) | 2022.02.23 |
| [통계] t-test (0) | 2022.02.23 |