각 개체에 대한 결과를 1 이나 0으로 나타내는 이항반응변수에 대하여 설명
성공할 확률을 나타냄
반응변수가 범주형변수인 경우 선형회귀분석은 적합치않음
1. 로지스틱회귀모형
로지스틱회귀모형은 확률의 로직, 즉 오즈의 로그갑에 대해 다음 같은 선형식을 가정한다.
1) 오즈
오즈 (odds) & 로짓 변환성공 확률이 실패 확률에 비해 몇 배 더 높은가를 나타내며 그 식은 아래와 같다.

예를 들어 성공확률이 0.8이라면 0.8/1-0.8 = 4 로 성공확률이 실패확률보다 4배 높다는 것을 의미함
2) 로짓변환
로짓 변환오즈에 로그를 취한 함수

오즈의 경우 실패확률이 아무리 커도 0에 가까운 반면 성공확률이 아주 클경우에는 무한대에 가깝게 된다.
그래서 서로 대칭을 맞추어 주기위해서 로그를 붙여준다
로그변환을 하면 0을 기준으로 대칭한다.
3) 로지스틱함수
로지스틱 함수의 그래프는 Figure 1과 같고 이는 독립 변수 x가 주어졌을 때 종속 변수가 1의 범주에 속할 확률을 의미한다. 즉, p(y=1|x) 를 의미한다.로지스틱 함수는 로짓
변환을 통해 만들어지고, 그 형태는 다음과 같다.

(출처) 위키백과

로지스틱함수는 우측 그래프같이 s자 모양을 띈다.
일반 회귀분석의 경우에는 기울기가 일정하지만 로지스틱함수는 기울기가 일정하지 않은 모습을 볼 수 있다.
2. 실습
데이터
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from statsmodels.formula.api import logit
crabs = pd.read_csv('crabs.csv')
crabs.head()| color | spine | width | satell | weight | y | |
| 0 | 3 | 3 | 28.3 | 8 | 3050 | 1 |
| 1 | 4 | 3 | 22.5 | 0 | 1550 | 0 |
| 2 | 2 | 1 | 26.0 | 9 | 2300 | 1 |
| 3 | 4 | 3 | 24.8 | 0 | 2100 | 0 |
| 4 | 4 | 3 | 26.0 | 4 | 2600 | 1 |
y값이 반응변수인 것 암컷이 부수체를 가지냐(1) 아니냐(0)
등딱지의 너비 width
model = logit('y~width', data =crabs).fit()
sns.scatterplot(x = 'width',y = 'y', data = crabs)
x_ = np.arange(crabs['width'].min(),crabs['width'].max(),0.01)
y_ = model.predict({'width':x_})
sns.lineplot(x = x_, y = y_, color = 'red')
plt.show()
model.summary()


상단의
로지스틱 회귀모형은 x가 1증가할 때 여기서는 (width) 로짓이 beta만큼 증가하는 것을 나타낸다
위 결과로부터 로지스틱회귀모형을 적합하면
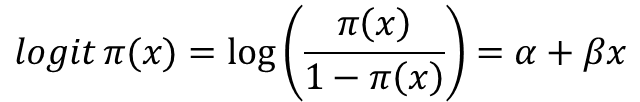
logit( pi(x) ) = -12.35(alpha) + 0.497*width(beta) 이다.
이를 정리하면
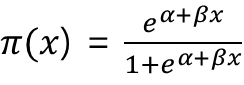
pi(x) = exp(-12.35 + 0.497 * width) / 1 + exp(-12.35 + 0.497 * width) 이다.
beta > 0 이기 때문에 너비값이 커지면 예측확률 은 커진다.
만약 여러가지의 독립변수들이 있었다면 우측의 p > |z| 값을 확인하면서 해당 변수가 종속변수의 변화에 유의한가를 확인 할 수 있다.
위의 width는 아주 유의한 것으로 확인된다.
model.predict({'width':21})0 0.129096
dtype: float64너비가 21 일 때의 부수체가 있을 확률은 0.129가된다.
혼동행렬
model.pred_table()array([[27., 35.],
[16., 95.]])
모형의 적합도 판단
model.aic198.45266392876505
'통계' 카테고리의 다른 글
| [통계] 시계열 분석, 분해법, arima (0) | 2022.03.11 |
|---|---|
| [통계] 단순선형회귀분석, 모형진단, 영향점분석 (0) | 2022.03.04 |
| [통계] 상관분석 (0) | 2022.03.03 |
| [통계] ANOVA 분산분석 (0) | 2022.02.23 |
| [통계] t-test (0) | 2022.02.23 |