과대적합과 과소적합을 해결하는 딥러닝학습기술
1. 모델의 크기조절
- 가장 단순한 방법
- 모델의 크기를 줄인다는 것은 학습 파라미터의 수를 줄이는 것
- 당연히 학습속도도 같이 커지거나 작아짐
- 파라미터의 수가 클 수록 과적합에 더욱민감하잼

model 의 경우 총 160,305개의 파라미터
model(small)의 경우 70,007개의 파라미터
model(big)의 경우 총 1,296,769개의 파라미터
2. 옵티마이저
- 확률적 경사하강법(SGD)
전체를 한번에 계산하지않고 확률적으로 일부 샘플을 뽑아 조금씩 나누어 학습
데이터의 수가 적어지기대문에 한 번 처리하는 속도는 빠름
손실함수의 최솟값에 이르기 까지 다소 위아래로 요동
단순하지만 문제에 따라 시간이 매우 오래걸림


- Momentum
운동량을 의미, 관성을 의미
이전의 속도를 유지하려는 성향
SGD보다 방향이 적게 변함

from tensorflow.keras.optimizers import SGD
optimizer = SGD(learning_rate=0.001, momentum=0.9)
# 모멘텀안주면 일반적인거 씀
- Nesterov
모멘텀의 방향으로 조금 앞선곳에서 그래디언트르르 구함
시간이 지날수록 좀 더 빠르게 최솟값도달

optimizer = SGD(lr=0.001, momentum=0.9, nesterov=True)
- AdaGrad
가장 가파른 경사를 따라 하강하는 방법
학습률을 자동으로 변화시킴
학습률이 너무 감소되어 전역최솟값에 도달하기 전에 학습이 빨리 종료되기도 하기댸문에 딥러닝에서 자제

from tensorflow.keras.optimizers import Adagrad
optimizer = Adagrad(learning_rate=0.01, epsilon=None, decay=0.0)
- RMSProp
adagrad를 보완하기위해 등장
합 대신 지수의 평균값을 활용
학습이 잘안되면 학습률을 키우고 너무 크면 다시줄임

from tensorflow.keras.optimizers import RMSprop
optimizer = RMSprop(lr=0.001, rho=0.9, epsilon=None, decay=0.0)
- Adam
모멘텀의 최적화와 RMSProp의 아이디어를 더한것
지난 그래디언트의 지수 감소 평균을 따르고(Momentum), 지난 그레디언트 제곱의 지수 감소된 평균(RMSProp)을 따 름
가장많이 사용되는 방법

from tensorflow.keras.optimizers import Adam
optimizer = Adam(lr=0.001, beta_1=0.9, beta_2=0.999, epsilon=None, decay=0.0, amsgrad=False)
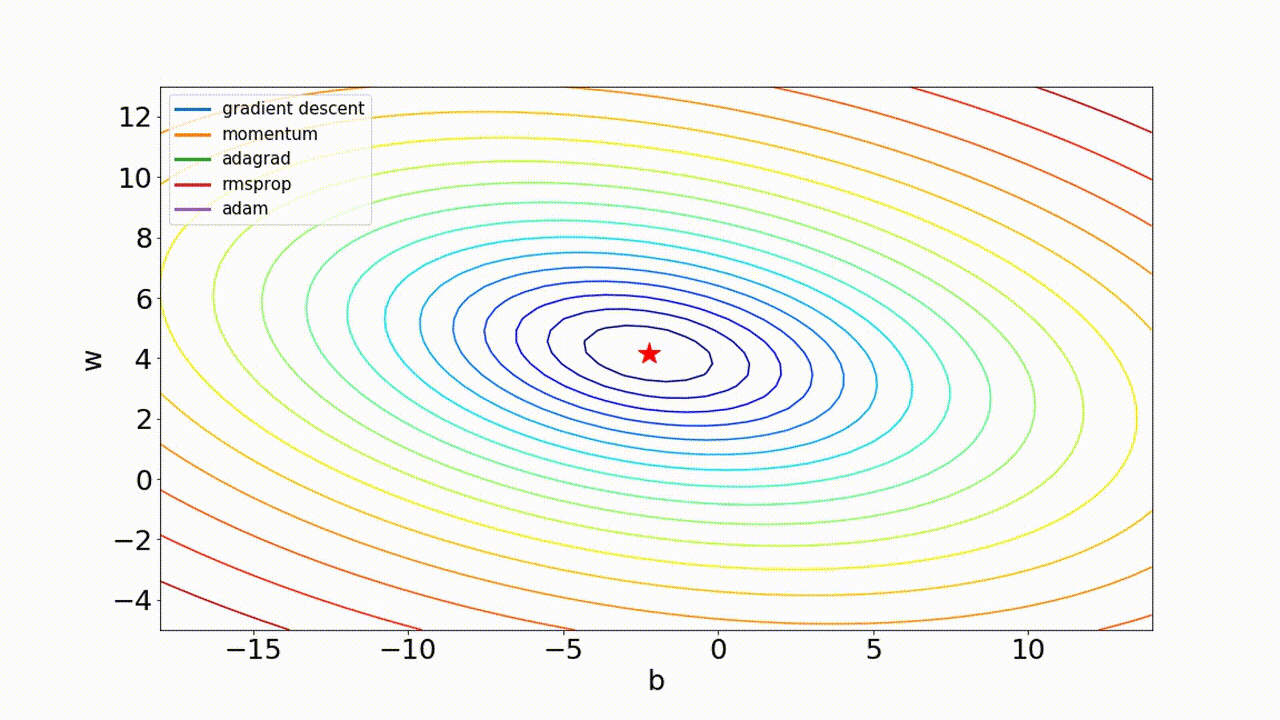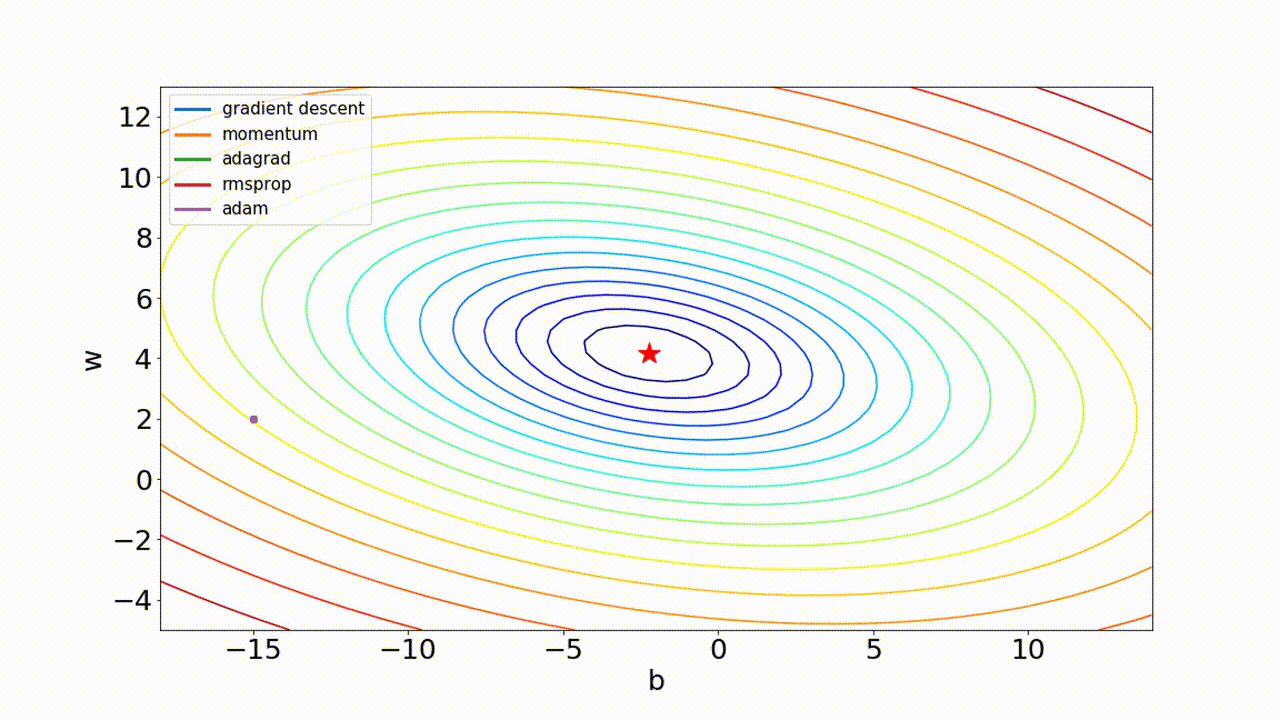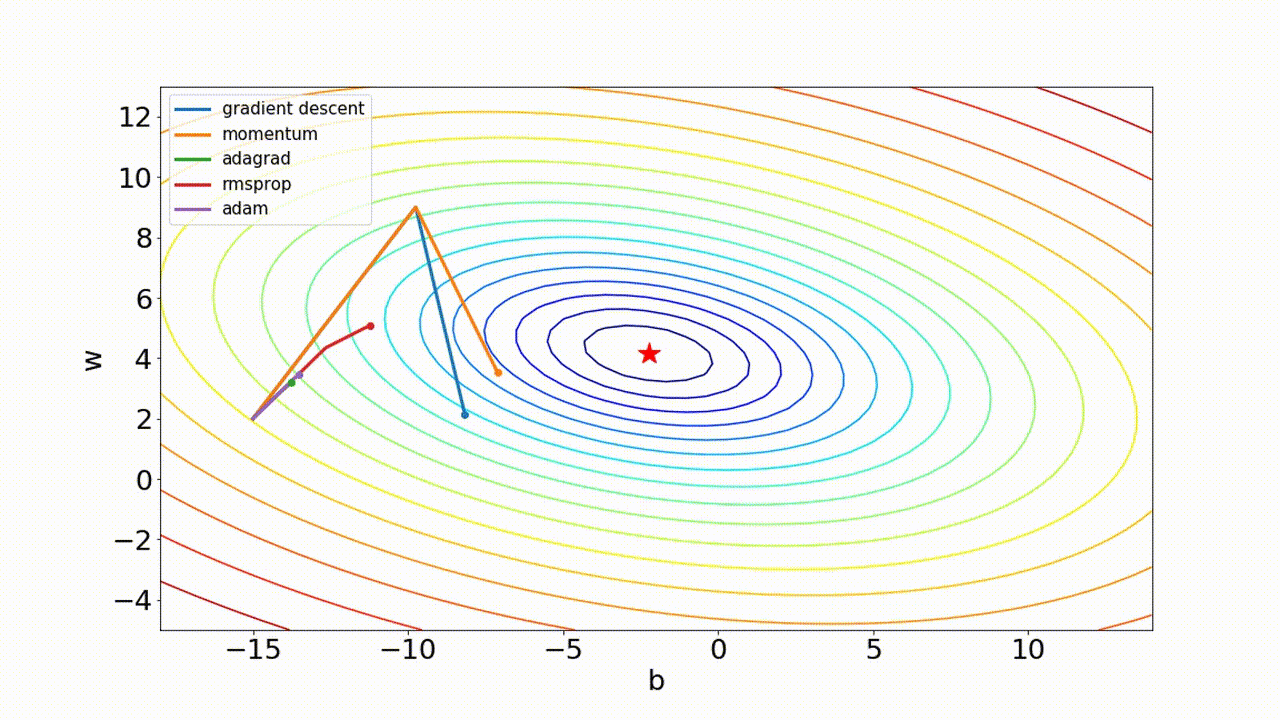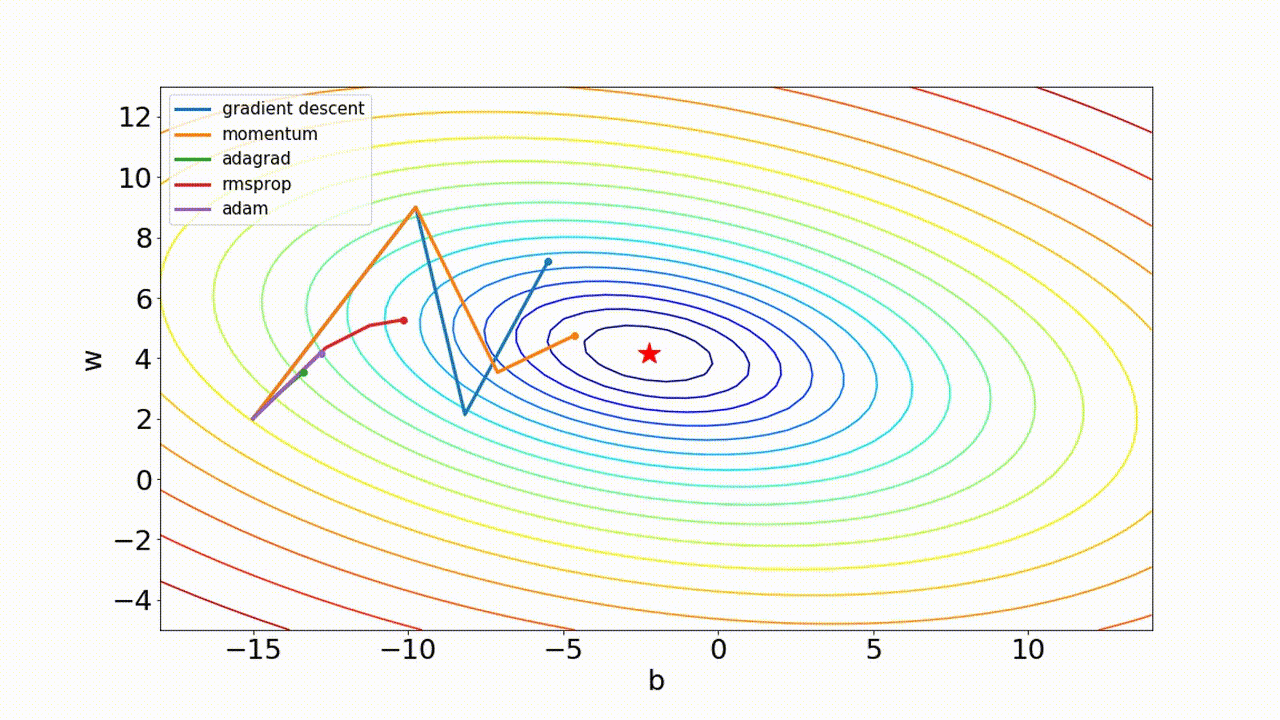
- 최적화 optimizer 비교
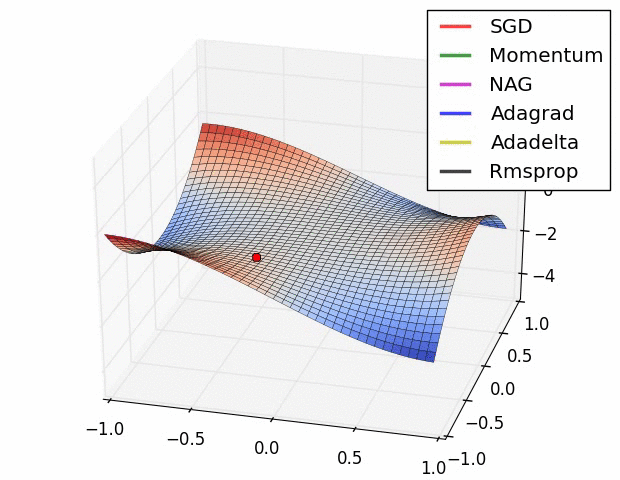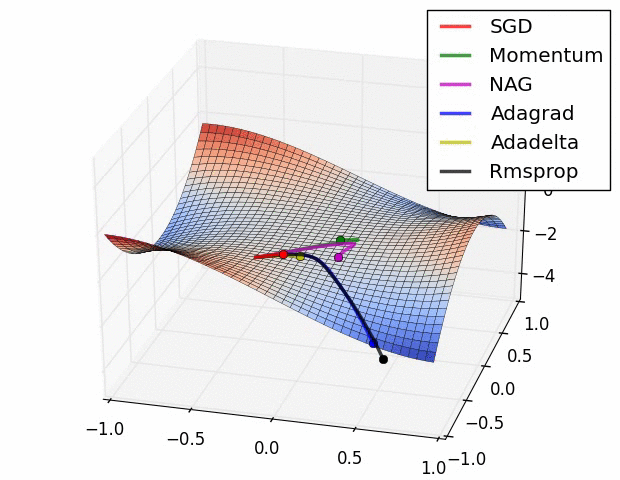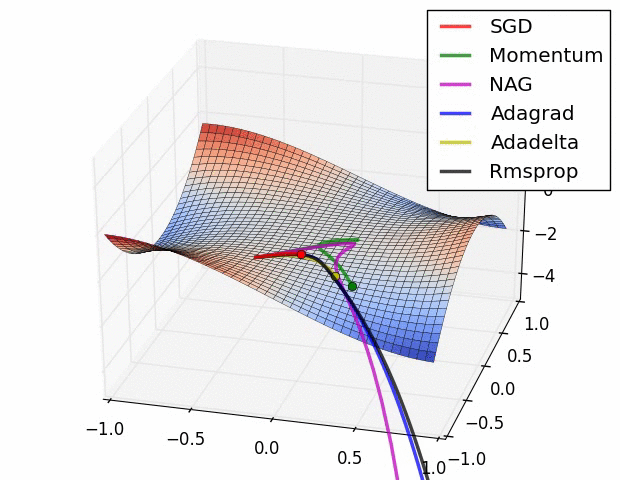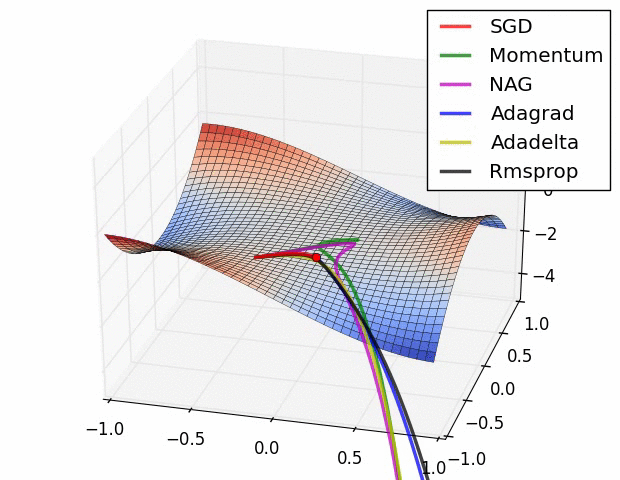
3. 가중치 초기화
- 가중치 소실
활성화함수가 선형일 때, 은닉층의 갯수가 늘어 날수록 가중치가 역전파되며 가중치 소실문제 발생
* 0~1사이로 출력되면서 0또는 1에 가중치값이 편중됨 이는 미분값이 0에 가까워짐을 의미
* relu 등장
- 가중치 초기화문제
가중치의 값이 치우쳐지면 표현 가능한 신경망의 수가 적어짐
따라서 활성화 값이 골고루 분포되는것이 중요
- Xavier (Glorot)
은닉층의 노드 수가 n이면 표준편차가 1/sqrt(n) 인분포
활성화함수가 선형인 경우 매우적합
- He
표준편차가 sqrt(2/n) 인분포
활성화함수가 비선형일떄 매우적합
Dense(1, kernel_initializer='he_normal')
Dense(1, kernel_initializer='glorot_normal')
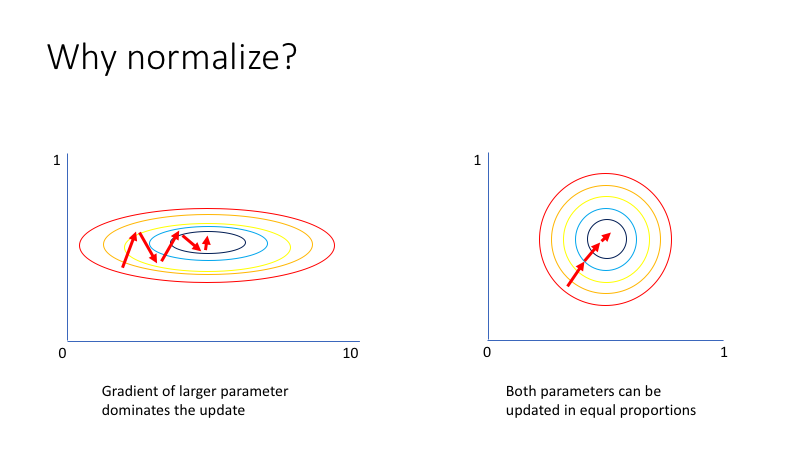
4. 배치 정규화
- 모델에 들어가는 샘플들을 균일하게 만드는 방법
- 가중치의 활성화값이 적당히 퍼지게끔함
- 학습을 빠르게 진행시킴
- 일반화성능ㅇ을 늘림
- 과대적합방지
- 주로 Dense또는 Conv2D 이후, 활성화함수 이전에 놓임
from tensorflow.keras.layers import BatchNormalization, Dense, Activation
from tensorflow.keras.utils import plot_model
model = Sequential()
model.add(Dense(32, input_shape=(28*28,), kernel_initializer='he_normal'))
model.add(BatchNormalization())
model.add(Activation('relu'))
model.summary()
plot_model(model)5. 규제 regularzation
- 과대적합(Overfitting, 오버피팅)을 방지하는 방법 중 하나
- 과대적합은 가중치의 매개변수 값이 커서 발생하는 경우가 많음
- 이를 방지하기 위해 큰 가중치 값에 큰 규제를 가하는 것
- 규제란 가중치의 절댓값을 가능한 작게 만드는 것으로, 가중치의 모든 원소를 0에 가깝게 하여 모든 특성이 출력에 주 는 영향을 최소한으로 만드는 것(기울기를 작게 만드는 것)을 의미
- 복잡한 네트워크 일수록 네트워크의 복잡도에 제한을 두어 가중치가 작은 값을 가지도록 함
- 적절한 규제값을 찾는 것이 중요
- L2 규제: 가중치의 제곱에 비례하는 비용이 추가(흔히 가중치 감쇠라고도 불림)
가중치의 제곱합
손실함수값에 일정값을 더함으로써 과적합을 방지
lambda값이 크면 규제가 커지고 반대는 작아진다
더 로버스트한 모델을 생성하므로 l1보다 더 많이 사용
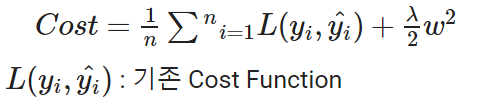
from tensorflow.keras.regularizers import l1, l2, l1_l2
l2_model = Sequential([Dense(16, kernel_regularizer=l2(0.001), activation='relu', input_shape=(10000,)),
Dense(16, kernel_regularizer=l2(0.001), activation='relu'),
Dense(1, activation='sigmoid')])
- L1 규제: 가중치의 절댓값에 비례하는 비용이 추가
가중치의 절대값합
l2규제와 달리 어떤 가중치는 0이되는데 이는 모델이 가벼워짐을 의미
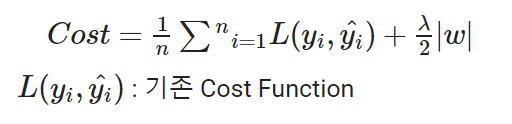
l1_model = Sequential([Dense(16, kernel_regularizer=l1(0.00001), activation='relu', input_shape=(10000,)),
Dense(16, kernel_regularizer=l1(0.00001), activation='relu'),
Dense(1, activation='sigmoid')])
- l1 l2 동시사용
Dense(16, kernel_regularizer=l1_l2(l1=0.00001, l2=0.001), activation='relu', input_shape=(10000,))
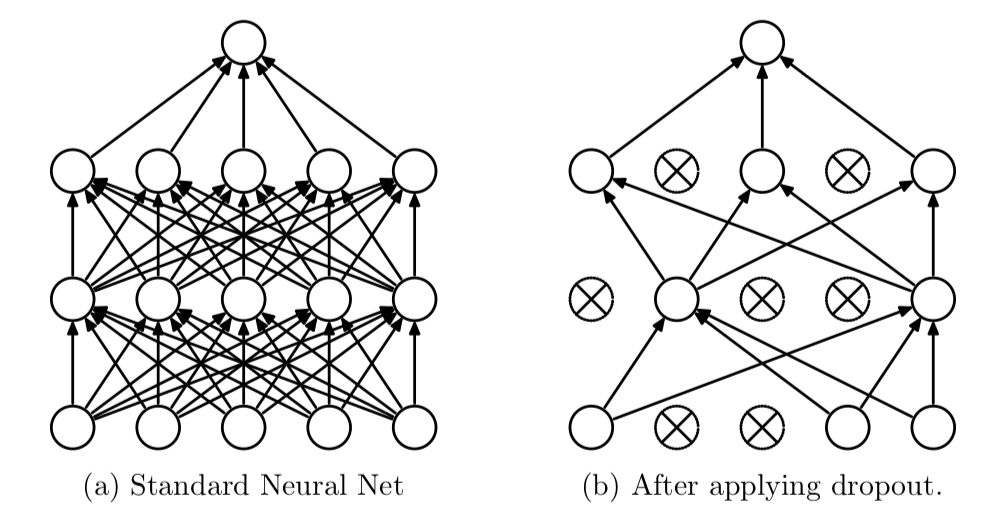
6. Dropout
- 신경망을 위해 사용되는 규제 기법 중 가장 효과적이고 널리 사용되는 방법
- 학습할 때 사용하는 노드의 수를 전체 노드 중에서 일부만을 사용
- 신경망의 레이어에 드롭아웃을 적용하면 훈련하는 동안 무작위로 층의 일부 특성(노드)를 제외
- 테스트 단계에서는 그 어떤 노드도 드롭아웃 되지 않고, 대신 해당 레이어의 출력 노드를 드롭아웃 비율에 맞게 줄여줌
dropout_model = Sequential([Dense(16, activation='relu', input_shape=(10000,)),
Dropout(0.5),
Dense(16, activation='relu'),
Dropout(0.5),
Dense(1, activation='sigmoid')])'TF' 카테고리의 다른 글
| [TF] CNN 컨볼루션 신경망 (0) | 2022.04.13 |
|---|---|
| [TF] 모델의 저장, callbacks (0) | 2022.04.11 |
| [TF] 모델 컴파일 및 학습 mnist (0) | 2022.04.11 |
| [TF] Layer, Model, 모델구성 (0) | 2022.04.11 |